Every topic that could come up in a GL 11 Plus Non-Verbal/Spatial Reasoning Exam
The key to success in a GL Non-Verbal Reasoning (NVR) 11 plus exam is practice. At first glance some of these questions will likely look more like some kind of newly-discovered alien language than an exam to test your child’s abilities, and it may make your child just want to give up before they’ve even started.
However, just a little bit of practice on a regular basis will allow your child to become familiar with these question styles. This, rather than full-scale tutoring, will give them what they need to do well in the exam, namely a good eye for detail as well as good discipline in reading and understanding the questions and double checking their answers for easily-made but costly mistakes.
If your child is taking a CEM exam, they will also have to prepare for NVR, and will likely encounter many of the same question types we see here, however this article will specifically deal with each of the 12 question types that usually appear in GL-made 11 plus exams.
Some schools and consortiums (though not all) also ask GL to incorporate Spatial Reasoning into their 11 plus exams. Click on the button below to skip to the Spatial Reasoning section.
Type 1 - Most unlike
In type 1 questions you are asked to find the odd one out in a series of 5 shapes.
Often to the naked eye it may appear that there is no odd one out, so this type of question requires looking for subtleties such as where each component of the figure is positioned, which way each component is facing relative to the rest of the shape and what colour each of them is.
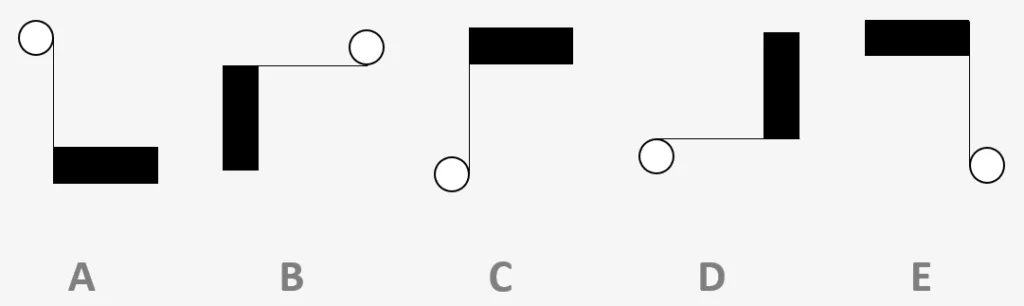
In the example question the odd one out is C because when we turn each of them so that they are facing the same direction, eg with the black bar at the bottom like in A, we discover that on C, the line and circle are are on the right hand side of the shape, whereas on the other four they are on the left.
Example Question:
Which figure is most unlike the other four?
Type 2 - Most like (3 figures)
On type 2 questions we are given a sequence of figures which have certain aspects in common, and we have to choose which of the five options we’re given will fit in to this sequence. Make sure that you check each of the options you are given, as often there are a number of similar options with only slight differences that catch people out.
In the example question we can see that the three figures in the sequence have a small shape within a larger version of the same shape. The smaller version has diagonal lines running from the top left corner to the bottom right. Therefore, the option that fits into this sequence is D, because while option C is also similar, the diagonal lines in the smaller shape in C are running in the wrong direction for this sequence.
Example Question:
Which one of the second five figures is most like the first three?

Type 3 - Most like (2 figures)
Type 3 is very similar to type 2, but here we are only given a sequence of two figures with which we have to find a third that will fit in. Again, remember to double check every option and work out the subtle differences that mean only one of them can be the correct answer.
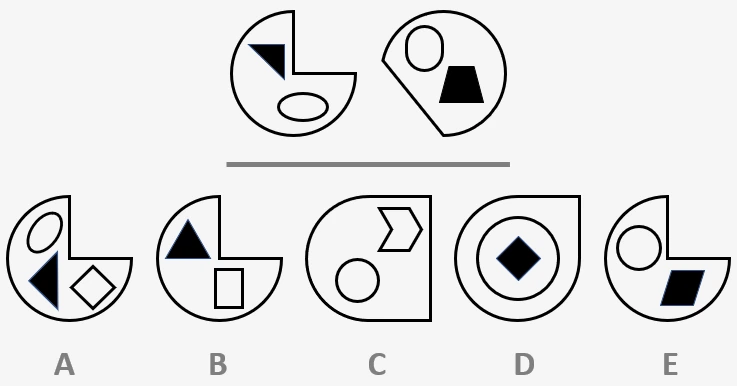
In the example question, we find that both of the figures in the sequence have a large shape (although not necessarily the same shape), with two smaller ones inside. The two smaller shapes are of a similar size, however one has curved edges and is white, and the other has straight edges and is shaded black. The only option that matches this description is E. B looks very similar at first however both of the smaller shapes have straight edges, so this cannot be the right answer.
Example Question:
Which one of the second five figures is most like the first two?
Type 4 - Series or sequences
In the fourth type of question we are given a sequence of shapes or patterns, with one missing. In this type of sequence, each figure has to follow on from the previous one in the series. For example, the figures in the sequence may all be exactly the same but facing different directions. Therefore the missing figure that we need to find won’t just be the option that is in the same style as the other figures in the sequence, but it will also have to follow the pattern.
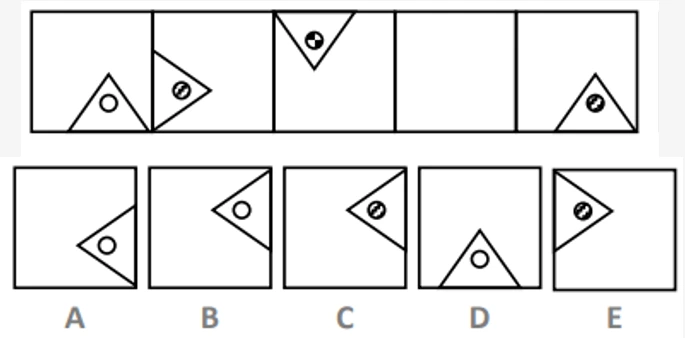
In the example question, we can see that the triangle rotates clockwise around the edge of the square, and that if it is on the top side of it, then it is placed slightly left of centre along the side. Therefore we narrow the correct answer down to options B and C as these would be the logical next step in the aforementioned pattern. As well as this, the small circle within the triangle is shaded differently for each square. We can thus work out that option B must be correct as the circles in the square either side of the missing box are both shaded, so this one must be a blank circle.
Example Question:
In the sequence below, one of the squares has been left empty. Work out which of the five figures should fill the empty square.
Type 5 - Extended series
Type 5 is similar to type 4, however we’re given a longer sequence, and two of the boxes are shaded in, making it more difficult to work out what the pattern is.
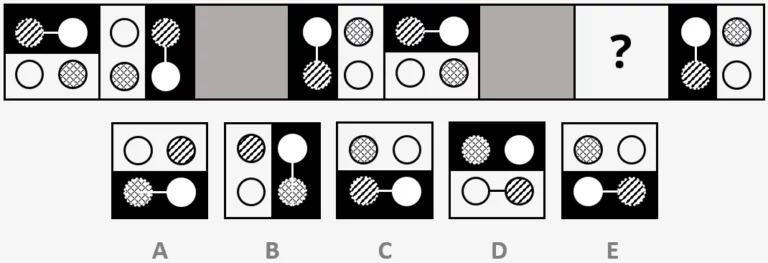
From what is there, we can tell that each box features the same pattern but each one is turned 90 degrees from the previous one. From that fact, we can work out that the box we need to fill will have its bottom half shaded black. Therefore we can rule out options B and D. Then we can rule out C as it has both of the shaded circles on the same side, whereas in the sequence they are always diagonal from one another. Lastly, if we turn one of the boxes in the sequence so that the black half is on the bottom, we can see that the circle with diagonal lines across it will be in the bottom right corner of the box. Therefore the answer must be E.
Example Question:
In the sequence below, two of the squares have been shaded in so you cannot see the pattern, and there is one square with a question mark.
Decide which one of the five squares on the bottom row should take the place of the square containing the question mark.
Type 6 - Triangle series
Type 6 is also similar to type 4, however with triangles instead of boxes.
In the example question, we can ignore the bottom three triangles in the sequence as these clearly have different shapes and colours to the top three and therefore must follow a different sequence. When we compare the two triangles on the top which aren’t missing, we can see that they both feature a small right-angled triangle of the same colour, however they are facing 180degrees in the opposite direction from one another. As a result, we can infer that the empty triangle, which is between them, will feature this same small, white, right-angled triangle, but at a 90 degree angle from the two that we can see. Therefore the answer is B.
Example Question:
Decide which of the five triangles on the bottom should take the place of the empty triangle in this sequence of six triangles.
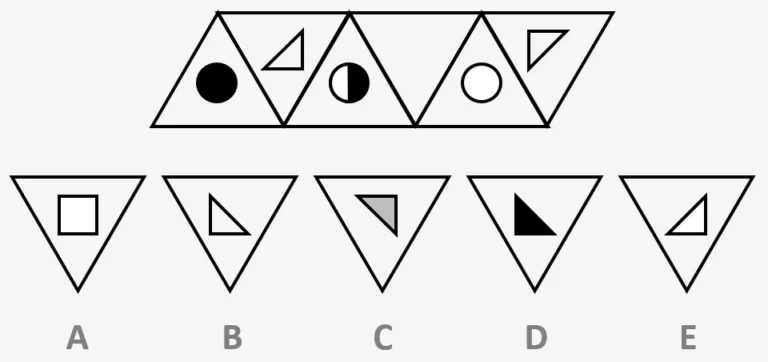
Type 7 - Analogies
In type 7 we’re given a pair of shapes that relate to each other in some way, and then are asked to find the pair of a third shape, from five options. Sometimes when working out a problem like this we have to rely on trial and error, as we might think we’ve worked out the pattern, and then find that none of the options we have to choose from follow the pattern that we’ve worked out. As a result, we can tell that the pattern we were using was not correct, and have to find another way that the first pair of shapes are linked.
In the example, we can see that the circle that we’re given is split into two black quarters, one white quarter, and one checkered quarter. Therefore, it corresponds to the second square in the first pair of shapes, which also contains two black quarters, one white quarter, and one checkered quarter. Consequently, we know to look for an option that is similar to the first square, which has two white quarters, one black and one checkered. Options A and D both fall into this category. However, in the pair of squares we can see that from one square to the other, the checkered quarter moves diagonally across, and as a result we can conclude that the answer is A, because on D the checkered quarter remains in the same place as in the circle we’re given.
Example Question:
Decide which of the five shapes on the bottom row goes with the third one on the top row to make a pair like the two on the left.
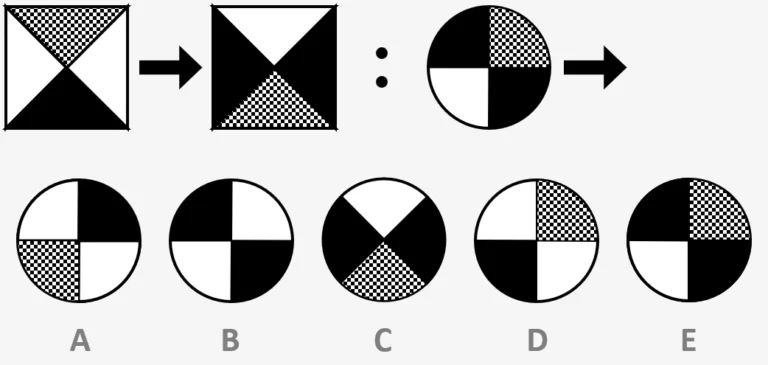
Type 8 - Matrices
In matrices we are given a big square, which is split into either 4 or 9 smaller squares, each containing some sort of figure set out in a pattern. One of these squares has been left blank and we have to use the remaining ones to work out which of the options we’re given is the correct one to fill it. If you’ve ever completed a sudoku puzzle then this should be a walk in the park for you.
In the example question, the matrix has 9 smaller squares, and each square contains a rectangle which is shaded one of three colours; white, grey or with diagonal lines. Each rectangle is also positioned in one of three ways; at the top of the box, in the middle, or at the bottom. Following these two rules about colour and position, there can be 9 options for what each box will look like. When we look at the matrix we can see that all of the 8 filled boxes are different, and therefore the box we’re looking for must be the only one of the 9 options which hasn’t already been used. Therefore we can conclude that the answer is A, because in the matrix there were only two grey rectangles, which were positioned at the top and in the middle respectively.
Example Question:
In the big square on the left, one of the small squares has been left empty. Work out which
of the five figures on the right should fill the empty square.
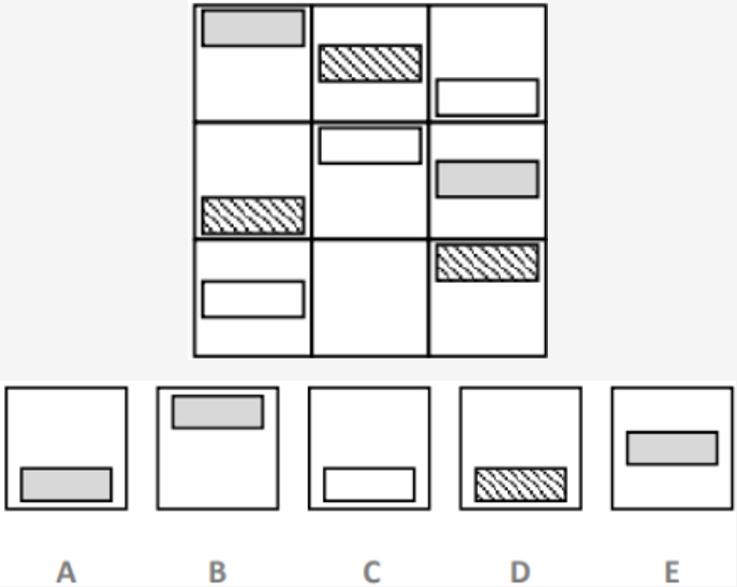
Type 9 - Similar triangles
In type 9 questions, we are given two large triangles, split into four smaller triangles each. These smaller triangles contain shapes that together form a pattern. This could relate to the number of sides of each shape, their colour, or just their relation to one another. We have to choose which of the five options we’re given can fit into the empty space on the second triangle. In order to do this, we have to first work out the pattern of the triangles.
In the example question, for the first segment of the first large triangle contains a quarter of a circle. Each of the following segments add one quarter to the circle until we have a full circle at the top. In the second large triangle we can we a cross at the top, and a quarter, then half a cross in two of the other segments. Therefore we know we are looking for three quarters of a cross to fill the final segment. We can conclude that the answer is C rather than E as the shape in E is rotated and therefore does not fit with the rest of the segments.
Example Question:
On the top row we have two large triangles, each made up of four smaller triangles. One of the smaller triangles has been left empty. Decide which of the five triangles on the bottom row should fill the gap.

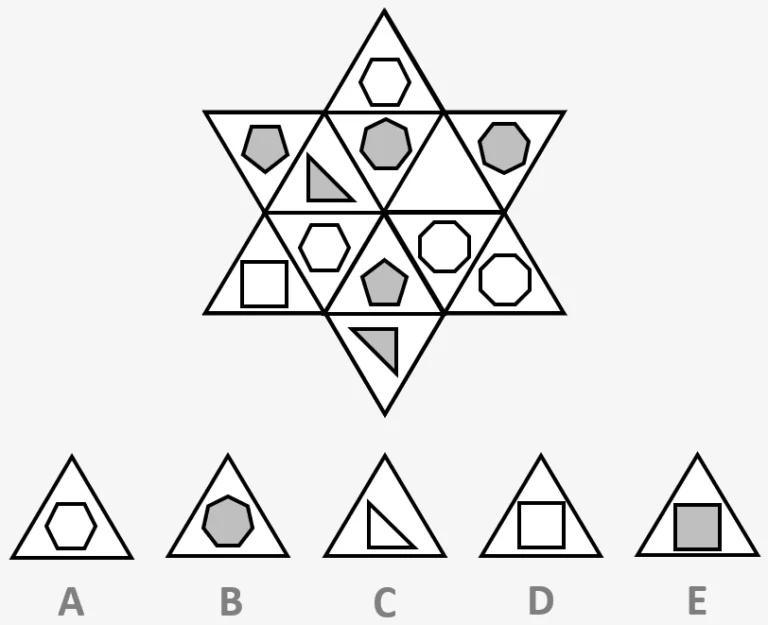
Type 10 - Star matrices
Here, we are given a six-sided star that contains 12 small triangles, each with a shape or figure. We have to work out the pattern that these shapes are in so that we can find the missing triangle from the set of options we’re given. There is a wide variety of possible patterns that can be used in this question type, and therefore we may have to apply trial and error to find a pattern that does work.
One of the simplest ways we can work out the example question is by seeing that the outer ring of triangles contains one of each shape with 3 sides, 4 sides, etc. up to 8 sides. The inner circle also contains these same shapes, with the exception of a 4 sided shape. Therefore we can narrow the answer down to D and E, which are squares. Now we have to work out the pattern of the colours. We can see that each of the shapes in the outer ring are the same colour as their corresponding shapes in the inner ring, for example the pentagons are both grey. Therefore we can infer that the answer is D because the square in the outer ring is white.
Example Question:
Decide which of the five triangles at the bottom should fill the empty triangle within the star.
Type 11 - Horizontal codes
In this type of question we are given four shapes along with codes that correspond to each of them, and are asked either to find a code for a given shape, or find the shape for a given code. The codes we are given refer to a certain aspect of their respective shapes. This could be what type of shape, what colour, what size, what position it’s in, it could refer to the different patterns within the shape or the number of lines or dots, or corners for each shape. There are many variables at play here.
However each code only contains three letters, each referring to one of these variables, meaning that the shapes will likely also contain variables that are not recorded in the codes, and are merely there as distractions. One of the best ways to work out the code is to look for which shapes have letters in common, for example if two of the codes contain the letter Y, we can look at what their two shapes have in common and thus work out what Y means in this code.
In the example question, we can see that two of the codes have G. Their two corresponding shapes both have three lines running across them, and therefore we can work out that the first letter of each code refers to the number of lines within the shape. Our test shape has two lines, and therefore we know it will start with an F because the third shape we are given also contains two lines and starts with an F. Next we can see that the last two shapes have a J as the second letter in their codes. The only thing they have in common is that they have one dot. The test shape has two dots, as does the second shape, so we can work out that the second letter of the code we are looking for is K. The only option that contains F and K is option D, which is therefore the answer.
Example Question:
On the left are some shapes and the codes that go with them. Find the correct code for the test shape from the set of five codes on the right.
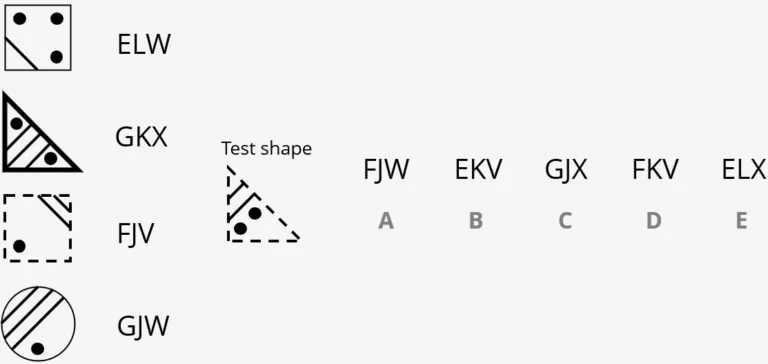
Type 12 - Vertical codes
The final question type in GL Non-Verbal Reasoning is vertical codes. This is largely similar to horizontal codes, except the codes only have two letters and the format is slightly different – but don’t let that scare you.
In the example question, the potential variables for the codes are the colour and position of the rectangles, as well as the position, length, direction and number of arrows. As with horizontal codes, our first clue is to look at which codes have letters in common. The second and fourth codes both contain B, and they also both have arrows which point up. Our test shape also contains an arrow that points up, so the first letter will be B. Next, the first and third shape both contain an O, and they both also have white rectangles, so the second letter of the code must refer to the colour of the rectangle. Our test shape has a grey rectangle, so the second letter for it must be N, because that is the second letter of the second shape, which also has a grey rectangle. Therefore the answer is option E, with the code BN.
Example Question:
In the boxes on the left are shapes and the code letters that go with them. Find the correct code for the test shape from the set of five codes on the right.

Spatial Reasoning
While still relatively uncommon, some schools and consortiums have begun to use Spatial Reasoning questions to supplement Non-Verbal Reasoning sections in their 11 plus exams. Spatial Reasoning seeks to test your child’s ability to find patterns as well as to imagine and manipulate 3-D shapes, for example by rotating or reflecting them, or by using cube nets.
Spatial Reasoning has only been used in 11 plus exams since 2015, and is currently only used in a small number of areas, including Kent, Lincolnshire and Buckinghamshire. However, some schools and consortiums have been known to use Spatial Reasoning questions within their Non-Verbal Reasoning exams.
There are 7 different types of Spatial Reasoning question that could come up in GL 11 plus exams, however most schools that use spatial reasoning do not use every type of question. Some consortiums make it clear beforehand what will be included, whereas for others it is less clear. Either way these types of questions do not require much preparation and are designed to be uncoachable so do not feel to concerned if you are unsure as your child’s preparation for the 11 plus exam should not look much different even if it is included.
Type 1 - Hidden Shapes
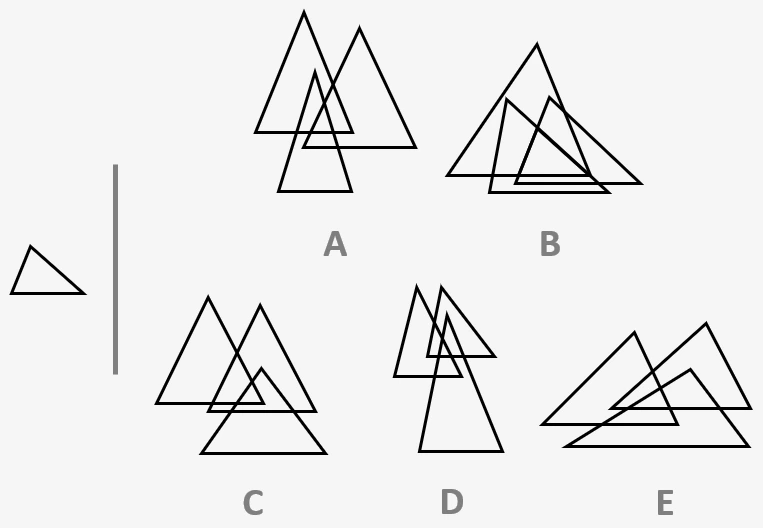
The first type of spatial reasoning questions involves searching for and identifying a given shape that has been hidden within a combination of other shapes. Sort of like Where’s Wally but with shapes.
The shape we’re looking for has not been altered in any way – it is exactly the same size and same way round as how it is given, we just have to search for it. It will often be hidden at an intersection of larger shapes.
We can see this in the example question, where the triangle we are looking for can be found within the intersection of three larger triangles on option B.
Example Question:
The shape on the left is hidden in one of the five shapes on the right.
All of its sides are visible in the shape where it is hiding and it is exactly the same size and same way round as it is presented on the left. Which of the five shapes contains the shape on the left?
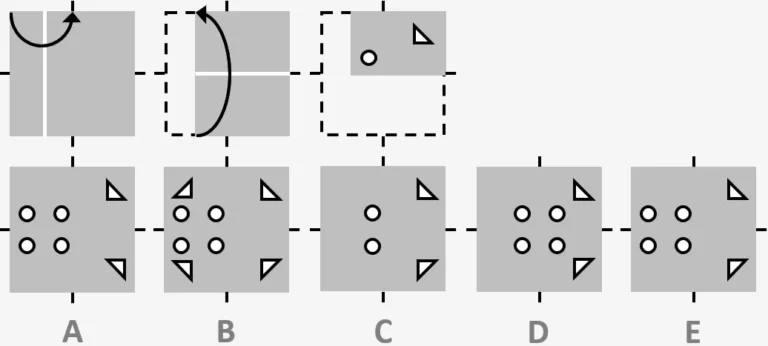
Type 2 - Figure Analysis
In type 2 questions, we are shown a square piece of paper being folded up in a certain way (which is different for each question), and then has had shapes punched through it. We have to work out what pattern will be formed by the shapes once the paper has been unfolded.
A trap that people often fall into is forgetting that if a piece of paper has been folded, the shapes on the folded side will come out upside down once it has been unfolded. In the example question this mistake might mean picking option A as the correct answer – which would be wrong as the bottom triangle (on the section that was folded over) should be the opposite way round to that. Instead, remembering that rule, as well as checking the measurement lines, is option E.
Example Question:
This question is about folding paper and punching holes in it. You must decide how the paper would look when it is unfolded. Choose which of the five squares beneath the folded squares shows how the paper would look when it is unfolded.
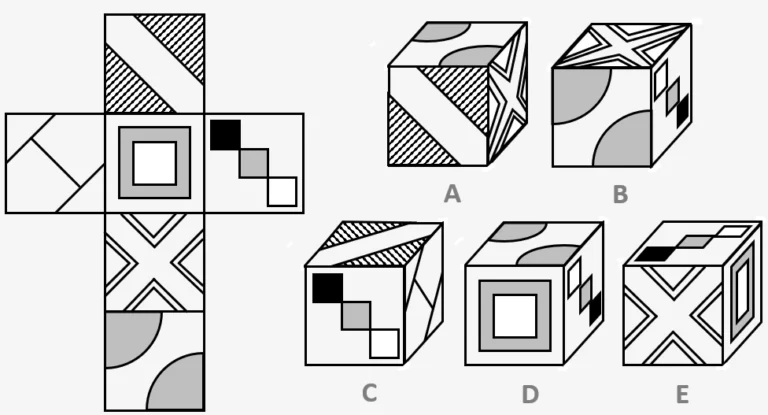
Type 3 - Cube Nets
In type 3 questions we are given a cube net upon which each square is given a different pattern. We have to work out which of the options we are given correctly shows how the cube should look once the net has been folded up. When choosing this we have to consider where each square on the net would be positioned relative to one another. As well as this, while some of the squares contain symmetrical patterns so will look the same whichever direction they are facing, others will have asymmetrical patterns meaning we will have to consider which options display them the right side up relative to the other squares.
One key to remember here is that squares which are two along from each other on the net will always be found opposite each other once the cube is made, and therefore cannot border each other. Therefore we cannot instantly rule out any of the options that contain two squares which should be opposite each other.
Example Question:
This question is about folding paper and punching holes in it. You must decide how the paper would look when it is unfolded. Choose which of the five squares beneath the folded squares shows how the paper would look when it is unfolded.
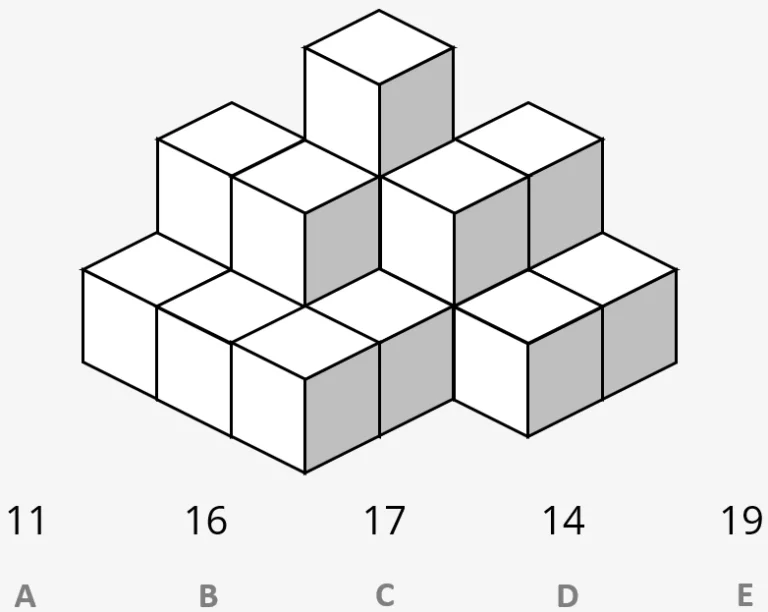
Type 4 - Block Counting
Block counting is the fourth type of spatial reasoning question. It involves counting how many blocks are in a pile of blocks that we are shown. This is challenging because we cannot see all of the blocks that make up the pile because some have been stacked on top of each other.
On the example question we can see that at the front of the pile there are 6 blocks which do not have any more stacked on top of them. Behind that are four blocks which are stacked on four more unseen blocks below (4+4=8). Behind that is one more block which is the top block in a stack of three (1+1+1=3). When we add these up we get 6+8+3= 17 – option C.
Example Question:
Each block in this pile is the same size and shape. Some blocks are hidden from view but must be there to hold the visible blocks up. Choose the answer that shows the total number of blocks in the pile.
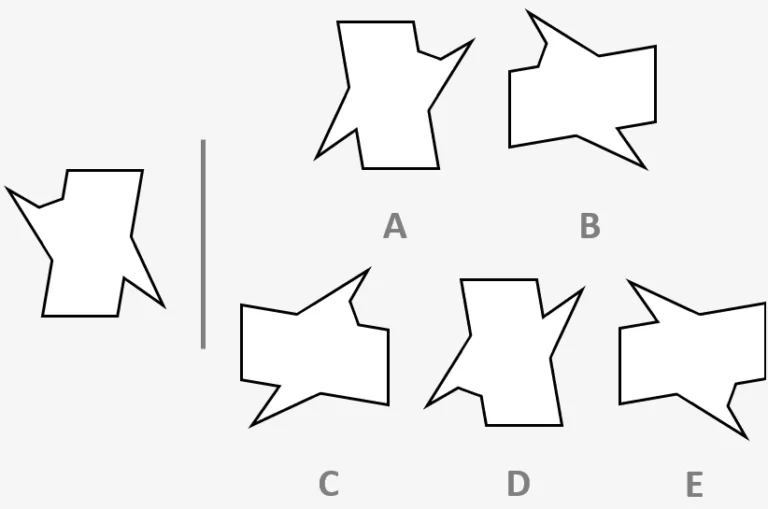
Type 5 - Matching Shape
Here we are given a test shape and five options which look similar to it. Only one of these options is exactly the same shape (but perhaps spun around to face a different direction), the other have been slightly altered or flipped over so that they may mirror the test shape but cannot make exactly the same shape without being flipped back over.
Essentially this question asks if you spun each option around on its own axis (in your head), would it make the same shape as the test shape? If yes, then it’s the correct option, if it makes something similar but perhaps with one bit facing the wrong way or positioned differently, then it is not correct.
When we apply this to each of the options in the example question, we find that the only option where the shape can be spun around to form exactly the same image as the test shape, is option C. To find this answer we must mentally spin around each option so that the central parallelogram is slants from the top right to the bottom left, as we see on the test shape. However, four of the five options have been mirrored, meaning that the parallelogram can only slant from the top left to the bottom right – and therefore no matter how much we spin them around on their own axis, they cannot form the correct shape – only option C can.
Example Question:
One of the five shapes on the right is identical to the shape on the left but has been spun around. The other four shapes on the right do not match the shape on the left because they have been picked up and flipped over, as well as possibly spun round. Choose the answer that shows the matching shape.
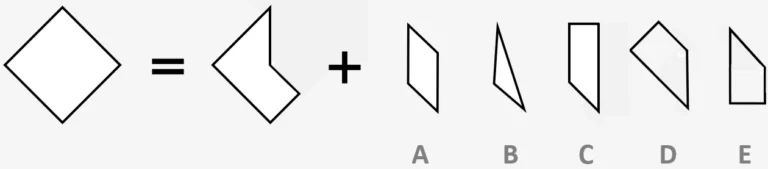
Type 6 - Jigsaw
In type 6 questions we are given one full shape, which we must then seek to recreate out of two puzzle pieces. The first puzzle piece is already given to us, and we must then complete the shape by choosing from 5 options. This type of question tests whether students can mentally arrange and map out the different pieces to find the whole shape, and is made tougher by the fact that the pieces may have been spun around so that you have to work out different ways it could fit into the shape.
In the example question, the shape we have to make is a diamond. The puzzle piece we are given gives us most of the diamond shape, but with part of the bottom right side missing, as well as the whole of the top right side of the shape. Therefore we can work out that we are looking for a four sided shape to complete the puzzle because we need to find two external sides of the shape as well as two internal sides where this piece fits in with the other piece we’re given.
We can also work out that the longest side of the missing piece must become the top right side of the finished diamond (connecting the right corner to the top corner), as that is the longest side that is missing from the piece we are given. As a result, we know which way round to try and fit each shape in, and from that can find that option D is the one that combines with the piece we’re given to form a full diamond.
Example Question:
In this question you have to add two jigsaw sections to form the complete shape on the left. From the 5 options, you have to find the missing section which forms the complete shape when added to the jigsaw section to the right of the equals sign. The missing section may have been spun around.
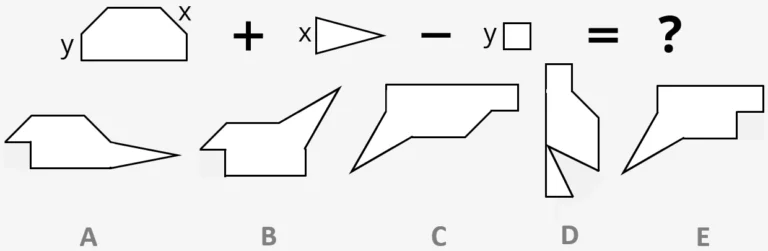
Type 7 - Combining Shapes
The final spatial reasoning question type that could appear on an 11 plus exam is questions about combining shapes. These questions are presented as an equation, in which shapes are added together or taken away from each other. Essentially, we are given a base shape, as well as shapes which we must add on to it, or remove from it. Certain sides on each shape have been assigned a letter which signals where they are to be added onto or removed from on the base shape. We have to choose from which is the correct final shape from 5 options.
In the example question we are asked to add a triangle to the top right corner of the base shape, and remove a square from the bottom left side of it. Therefore we need to look for the answer that exhibits this, without putting the shapes in the wrong places or adding them where they should be subtracted, or vice-versa. Therefore the answer must be option B.
Example Question:
Complete the following equation by adding or subtracting the shapes together. The shapes are marked by one or more of the letters X, Y, Z. The sides with matching letters must meet. Choose the answer that shows the combined shape. The final combined shape may have been rotated from its original position.
And there we have it, all of the possible types of question that could come up in a GL Non-Verbal and Spatial Reasoning paper. Remember to check out all of the question types and topics from the other 11 plus subjects here.
As we have previously said, the best way to prepare for this type of exam is with regular, focused practice. Our Fundamentals Subscription is the perfect way to do this, and it covers all of the GL 11 Plus subjects and topics. Check it out here.
