Every topic that could come up in a GL 11 Plus Maths Exam
Across all of the 11 plus exam boards (including GL and CEM), the skills and topic areas tested in the Maths section of the exam closely follow the Key Stage 2 National Curriculum. Therefore it should all be relatively familiar to your child when they sit their 11 plus exam at the beginning of year 6.
However, it is still very important to get ample preparation in before the exam, in order that your child feels sufficiently confident in each of the topic areas. As well as this, while each exam board follows the same general curriculum, the questions may be formatted differently to each other, and in ways that are unfamiliar to your child. This article will explain each of the different types of question that can be included in GL 11 Plus Maths exams, and show examples of what they may look like.
Type 1 - Place value and rounding
The first 11 plus maths topic involves being able to identify what each digit in a number means (for example knowing that 6 stands for 600 in 7657) as well as being able to round up or down to the nearest whole number, 10, 100 or 1000. The key thing to remember here is that if the digit we are rounding is a 5 or above, we round up, whereas if it is a 4 or below, we round down. For example if we were to round 6.374 to the nearest whole number, we would round it to 6. We know this because when rounding to the nearest unit, we have to look at the value directly to the right of it (which is the tenths), therefore in this example we look at the 3 in 6.374 to know to round down.
In the example question below, we’re asked to round 4579 to the nearest hundred. When rounding to the nearest hundred we know that if the number we’re rounding ends in 50 or above, it means we have to round up rather than down. Therefore we can round 579 up to 600, and we get our answer: E (4600).
Make sure you read the question properly and don’t accidentally round it to the nearest ten (4580) or thousand (5000).

Type 2 - Place value and rounding
These questions test your child’s ability to identify large numbers, for example if they be able to identify that 10,000,000 means ten million, or that 132,000 means one-hundred and thirty two thousand.
Type 3 - Standard addition, subtraction, division and multiplication
The core skills of KS2 Maths. This includes calculations involving brackets, negative numbers, fractions and decimals, among other complex concepts. If your child gets regular practice of the full range of these questions, they should not be too much of a problem come exam day.
In the example question, we know thanks to BODMAS that we have to do the calculation within the brackets first, so 7 – 31 = -24. In any multiplication or division, if one number is negative and the other is positive, the answer must always be a negative, whereas if both numbers are negative (or both are positive), the answer must always be positive. In this instance, we have two negative numbers (-24 x -5) so we can essentially treat them as positives. 24 x 5 = 120, so the answer is E.

Type 4 - Function/number machines
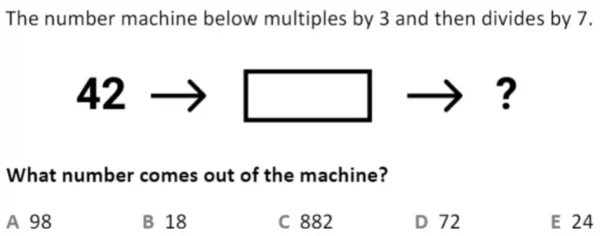
Number machine questions (also known as function machines) involve putting a number into a machine that has a certain function, and working out what will come out of it.
In the example below, the machine’s function is to multiply numbers that go into it by 3, and then dividing them by 7. Therefore, when the input is 42, we can work out 42 x 3 = 126 and 126 ÷ 7 = 18. Therefore B is the correct answer as 18 is what comes out of the machine.
Type 5 - Understanding the use of brackets (BODMAS)
BODMAS (Brackets, Order, Divide, Multiply, Add, Subtract) is an acronym that helps us to remember the correct order to complete a complex equation in. First we work out anything inside brackets, followed by divisions and multiplications, and finally additions and subtractions.
Following the BODMAS rule, we know that to complete the equation below, we must first complete the parts within the brackets. In the first brackets we find 77 x 52, which is quite a tough multiplication to do in our head, so a good way to break it down is by using Partition Method, meaning that we split up the numbers into 70 and 7, and 50 and 2, and multiply the first two by the last two. 70 x 50 = 3500, 70 x 2 = 140, 7 x 50 = 350 and 7 x 2 = 14. Then we add all of them together: 3500 + 140 + 350 + 14 = 4004, so 4004 is in the first brackets. We then repeat the process for the second set of brackets to get 1196. All that’s left now is to add 4004 and 1196 together to get the answer of 5200, or option D.

Type 6 - Inverse operations
Inverse operations are when we are given an equation with a missing segment and have to work out what’s missing based upon the parts that we are given, as well as the answer. Another word for inverse is opposite, which helps us to remember that in these questions if the calculation involves multiplication, we have to do the opposite function, divide, in order to find the missing part. Equally if the calculation involves addition, then we have to use subtraction to find the missing part.
In the example question, as well as inverse operations, we are also dealing with fractions. Therefore first we have to find a common denominator as they are currently different. 15 is a multiple of 5 so we can just multiply the numerator and denominator is 2 4/5 by 3, to make it 2 12/15. The calculation involves addition, therefore in order to find what’s missing we can subtract 2 12/15 from the answer to the calculation, 3 2/15. We are left with 5/15, which can be simplified to 1/3, therefore we know that the missing section is option A.

Type 7 - Factors and multiples: divisibility rules, & prime factors
Factors are numbers that divide exactly into another number, without leaving a remainder, for example 1 and 2 are factors of 4 because 4 ÷ 4 = 1, and 4 ÷ 2 = 2. A prime factor is a factor of a number that is also a prime number. For example, while 15 is a factor of 30, it is not a prime factor because it is divisible by 5 and 3, whereas 2, 3 and 5 are all prime factors of 30 because they do not have any of their own factors.
Multiples are basically the opposite of factors, and can also be referred to as times tables, for example 4, 6, 8, 10 are all multiples of 2.
In the example question we are asked to find which of the five options is a multiple of 13, meaning we can divide it by 13 and not be left with a remainder. Because we are working with large numbers here, if you struggle with multiplication try to find easier multiples that are nearby. For instance we can easily work out that 13 x 10 = 130, and then work out from that that option C, 106 is not a multiple of 13 because it is 24 away from 130, and 24 is not a multiple of 13. Similarly, 20 x 13 = 260, so we know that option A, 281, cannot be a multiple of 13 as it is 21 away. It can’t be option B because 13 x 6 = 78. We can find 15 x 13 by halving 130 to get 65, and adding that to 130 to get 195. From that we can work out that option D, 208, is 13 away, so it is a multiple of 13.
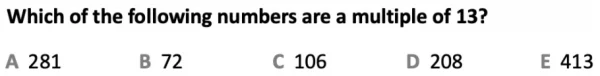
Type 8 - Highest common factors and lowest common multiples
Common factors are factors that are shared by more than one number, for example a common factor of 12 and 16 is 2. The highest common factor is the largest common factor that can be found for two numbers. While 2 is a common factor of 12 and 16, it is not the highest common factor because another common factor, 4, is larger.
11 plus papers are always multiple choice, therefore in difficult maths questions we can focus on the options we are given. In this case, we have to find a number which is a multiple of both 7 and 13. Options A (26), C (65), D (143) and E (247) are not divisible by 7, so we can rule all of those out, and conclude that the answer must be B, 182.

Type 9 - Number sequences & number patterns
In this type of question your child will have to identify patterns in both number sequences and illustrated patterns, in order to identify the next part of the pattern.
Harder questions may involve finding and using the nth term of a pattern. The nth term is a formula that allows us to find any term in a sequence. For example the nth term of 3, 7, 11, 15 is ‘4n-1’, because the pattern goes up in 4s, but starts at 3 rather than 4 so is -1. With this knowledge we can find numbers much further along in the pattern without writing out the whole pattern, for example we can quickly find out that the 23rd number in the above pattern is 91, because (4 x 23) – 1 = 91.
In the sequence below we can work out the pattern by finding the difference between each number. 81 – 64 = 17; 64 – 49 = 15; 49 – 36 = 13. For each number in the sequence, the difference is 2 smaller than the previous gap, meaning that the next number in the sequence must be 11 less than 36. Therefore the answer is E, 25.

Type 10 - Money & cost calculations
Perfecting this next type of question will come in handy for when your child is using their lunch card to buy their own food at secondary school. Fortunately our money was decimalised back in the 1970s, meaning that money and cost calculations are just simple additions now, which your child can become confident in with sufficient practice.
In the example, we are asked how much money two friends spend altogether. Kevin spends £0.99 on a vanilla cone and £1.50 on a hot dog while Jason spends £1.85 on a burger. 0.99 + 1.5 + 1.85 = 4.34, so the answer is D, £4.34.

Type 11 - Fractions
They key thing for your child to remember about fractions is to not be afraid of them! They may look complex and confusing but with regular practice you’ll be able to tackle them without even thinking about it.
A range of different questions relating to fractions may come up in your child’s 11 plus exam, including adding, subtracting, multiplying and dividing by them, as well as converting them to decimals or percentages, ordering them and simplifying them. The best way to make sure you cover every type of question about fractions is by getting an 11 plus preparation subscription as over time it will provide your child with regular practice of every type of question for each topic.
If you want to help your child this way, check out our subscription options here.
In this example question we’re given the answer and must choose which of the five options is the correct calculation for it. With BODMAS we know that we must solve the multiplication inside the brackets first, before doing any other part of the calculation. Each of these involve multiplying a number by a fraction, which in practice actually means we have to divide it by the denominator of the fraction, and then multiply it by the numerator. For example for option A, we would do 120 ÷ 5 = 24, and then 24 x 1 = 24. We then can focus on what is outside of the brackets, and do 4 x 24 = 96. Therefore we can rule out option A.
While we could repeat this process for each option, and for some questions we might have to, in this particular question we can see that the numbers involved in the final multiplication (outside of the brackets) must be factors of 85. Therefore we can rule out every option except for the answer, option D, as the only factors of 85 are 1, 5, 17 and 85, and only option D involves multiplying by one of these.

Type 12 - Decimals
Similar to with fractions, a range of questions involving decimals came up, including various calculations involving them and converting decimals to fractions or percentages.
The example question shows a simple calculation with both adding and subtracting of decimals. The first section of the calculation is 34.2 + 3.3, which equals 37.5. Then we have to remove 5.8 from this number, meaning we end up with 31.7, which is option D.

Type 13 - Percentages
There are a range of scenarios that percentages can be applied to, meaning that some percentage questions may appear more complex than the questions involving fractions and decimals. However at their core, these questions are not so different, and the key is just to focus on the numbers rather than the extra information we’re given.
In the example question, we know that 20% is the same as 1/5. Therefore to find 20%, we can do 212 ÷ 5 = 42.4. Yukon bought the bed for a 20% discount, so we need to remove 42.4 from 212, to find 169.6, or £169.60, option C.

Type 14 - Ratio, proportion & scale
One of the keys to mastering ratio questions is to remember that ratios can easily be converted into fractions.
In the example question, we have to work out how much sugar is needed for a Bakewell tart recipe. We are given the total weight of the ingredients as well as the ratios of the three ingredients involved; 4 : 4 : 3. If we add all three numbers in the ratio we get 11. Therefore we can divide the total weight of the ingredients (330g) into 11 portions of 30g. In the 4 : 4 : 3 ratio, the 3 represents the amount of sugar so we can do 30 x 3 to find the amount, which is 90g, option B. Sounds delicious 😋

Type 15 - Algebra & equations
If your child isn’t confident in maths, algebra can sound like a scary word. However, with regular practice and perhaps a bit of patience and self-belief, your child can become a pro in 11 plus-level algebraic equations.
In the example question we are asked what is the largest number x could be. “x” just stands for a number, one that we don’t know – it’s our job to find what it is. Due to the < 21, we know that altogether, 2x + 5 must be equal to 20 or less. Working back from that, we can take away the 5 to get 15. 2x just means x multiplied by two. 15 is not a multiple of 2 so we can instead conclude that the highest number x can be is 7 (option D), as 7 x 2 = 14.

Type 16 - Special numbers
This involves knowing the definitions of certain terms, as well as how to use them in calculations. These include:
Even and odd numbers: Even numbers are numbers that can be shared equally between two groups, for example 2 can be split into 1 + 1. Odd numbers cannot be split into two equal groups, for example 3, an odd number, can only be split into 1 + 2.
Prime numbers: Numbers that have exactly two factors, themself and one. These include 2, 3, 5, 7, 11. 1 is not a prime number because it only has one factor.
Square numbers: These are formed when a number is multiplied by itself. For example if we want to find the square of 4, then we do 4 x 4 = 16. This can also be presented as 4².
Square roots: This is when we take a square number and find what it is the square of. For example the square root of 9 is 3, because 3 x 3 = 9. This is basically the same process as finding a square number, but backwards, and it can be presented as √9 = 3.
Cube numbers:These are formed when a number is multiplied by itself 3 times. For example 2 x 2 x 2 = 8. This can also be presented as 2³. We can also find cube roots, for example ∛8 = 2.
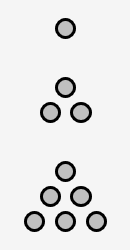
Triangular numbers: Triangular numbers are numbers that can be represented as a triangle of dots. These include 1, 3 and 6. The gap between two triangular numbers increases by one each time, for example between 3 and 6 there is a gap of 3, and between 6 and the next triangular number, 10, there is a gap of 4, and so on.
Indices: This refers to when a number is raised to the power of another number. For example 6⁵ = 6 x 6 x 6 x 6 x 6 = 7776. In this example the index (singular of indices) refers specifically to the ⁵ in 6⁵.
Roman numerals: I, II, III, etc. Key things to remember are that 4 isn’t IIII, but instead is IV, and 9 isn’t VIIII, but instead is IX.
Negative numbers: Numbers below 0. Some of the key rules to remember with negative numbers is that when two are multiplied together or divided by each other
Consecutive numbers: Numbers that follow on from each other in order, for example 1, 2, 3, 4, or 56, 57, 58, 59. Questions involving consecutive numbers will ask things like ‘find five consecutive numbers that add up to 45’. The numbers we’re looking for will likely be around 1/5 of 45, which is 9. Therefore we can try all of the numbers around 9. 7+8+9+10+11 = 45, so these are the correct numbers.
In this example question we’re looking at prime numbers. The first five prime numbers are 2, 3, 5, 7 and 11, which we’re told make 28. We need to add the next two prime numbers to this. They are 13 and 17. So 28 + 13 + 17 = 58, so the answer is option A.

Type 17 - Problem-solving
This is another question type where the key is to just have a bit of patience, practice regularly, and also have an eye for detail to make sure that they’ve included every step that the question asks. You should always double check your answers, however this practice is particularly important on longer questions like this in order to avoid making silly mistakes.
This example question shows two students’ dilemma as to what time they must leave home in order to be on time to school. They live 5 minutes from Bellingham train station and must get to Orpington before 9am. The latest train they can get that gets into Orpington before 09:00 (08:50) doesn’t stop at Tasmin and Taha’s station, therefore they would have to get the train before that, at 07:30. The question tells us they have a five minute walk to the station, therefore they would have to leave home at 07:25, option B.

Type 18 - Angles and lines
This involves being able to identify and understand different types of angles, triangles and lines.
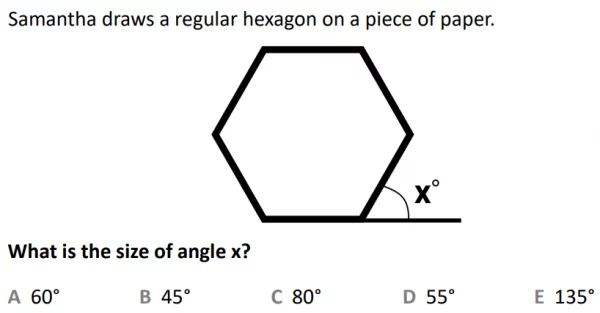
In the example question we are shown a regular hexagon and are asked to work out the size of an angle beside it. We know that all of the angles in the hexagon are equal, so we can use the following equation to work out the size of the internal angles: 180°(n−2) / n, where n = the number of sides in the polygon in question.
This formula works because 4 triangles can fit into the hexagon, as shown on the right. All of the angles in any triangle add up to 180°, so all of the angles in our hexagon will add up to 4 x 180 = 720°. To find the size of each individual angle we just divide 720° by how many there are (6), which gives us 120° each.
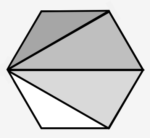
Therefore 180°(6−2) / 6 = 120°. The angle we are searching for is exterior to the hexagon and running in a straight line from one of the sides. Therefore we know that the combination of our angle and the internal angle will add up to 180°. 180° – 120° = 60°, so the answer is option A.
Type 19 - 2D shapes
This mainly involves identifying obscure shapes, such as kites, parallelograms and rhombuses from descriptions. However knowledge of 2D shapes will also come in handy for other types of questions, such as questions about areas, perimeters or angles in shapes.
In the example question we have to identify what type of shape Ranjith has drawn from a short description. A kite does not have any parallel sides, while a rhombus, parallelogram and rectangle each have two pairs of parallel sides. Therefore the answer can only be C, a trapezium.

Type 20 - 3D shapes
Similarly, questions about 3D shapes may simply mean identifying different types of shapes such as cylinders, pyramids or prisms. Another important skill to have is the ability to mentally visualise 3D shapes as they may not be able to be accurately represented on paper.
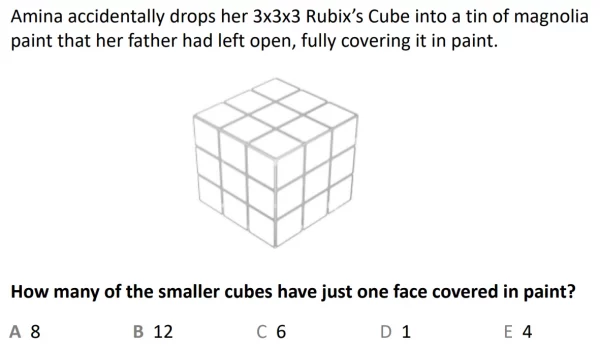
In the example question we’re shown a 3x3x3 Rubik’s Cube, which has been dropped into paint. We have to work out how many of the smaller cubes would only have one side that is covered in paint. As we can see in the diagram, on each side of the Rubik’s Cube only one smaller cube has one face showing, as the others are all at a corner and therefore have 2 or 3 faces showing. Therefore we can identify that since all cubes have 6 sides, there must be 6 smaller cubes altogether where only one face is covered in paint, so the answer is C.
Type 21 - 3D shapes
Lines of symmetry are when you can draw a line down or across something and the same image or pattern will be mirrored either side of the line. Rotational symmetry is when a shape or pattern can be rotated in a way that means it will look exactly the same as it did before it was rotated.
In this example question we are asked which of the words has a vertical line of symmetry, meaning a line can be drawn vertically down its centre and either side of it will be mirrored. Therefore we can identify option C, TOOT as the correct word as the same letters are mirrored on each side: TO | OT. Other questions in 11 plus exams may ask for horizontal symmetry, so make sure to read the question correctly so that you can identify the right type of symmetry.

Type 22 - Area and perimeter
This involves being able to remember the formulas to find the areas and perimeters of shapes like squares, rectangles, triangles and circles, as well as more complex shapes like irregular quadrilaterals and shapes with more than 4 sides. Sometimes these questions may be complicated by the use of compound shapes, where two shapes (often rectangles of different sizes) are stuck together and we have to work out the areas to both and then add them together.
This example question asks us to find the area of a parallelogram. While at first this may look daunting, if we remember the rule of how to find the area of a parallelogram, it is quite simple as we just need to multiply the height (3m) by the width (10.5m), and we can ignore the diagonal side. 3 x 10.5 = 31.5, so the correct option is option E, 31.5m°.

Type 23 - Measurement
These questions test two things; calculations regarding length, mass, volume and capacity, and also your child’s understanding of what different units of measurement mean, including both metric and imperial measurements.
In the example question we’re asked what the cost per mile of a 110 mile journey is. We’re told that fuel costs £1.15 per litre and that a 110 mile uses 22 litres of fuel. Therefore we start by working out how much the journey cost overall by multiplying 1.15 (cost per litre) by 22 (amount of litres used in the journey), to get £24.8. Then to find the cost per mile we divide this by 110 to get 0.23, so the answer is option E, £0.23.

Type 24 - Marking & interpreting scales
These questions involve being able to identify numbers on a number line, often without being told what the scale is, and having to work it out based upon what is at either end of the scale, and how many sections it has.
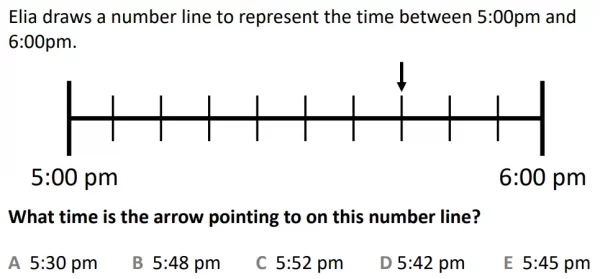
In the example question we’re given a number line between 5pm and 6pm, with an arrow pointing to a certain time which we must identify. First of all we must work out what the scale of the number line is. From 5pm to 6pm there are 10 subdivisions. As a result we can work out 60 (minutes) ÷ 10 = 6. Therefore each segment must represent 6 minutes. The time we need to identify is 3 lots of 6 minutes before 6pm. 3 x 6 = 18, so the arrow is 18 minutes before 6. 60 – 18 = 42. Therefore the answer is option D, 5:42pm.
Type 25 - Coordinates
Questions to do with coordinates can test your child’s ability to identify coordinates, as well as their ability to mentally rotate, translate and reflect shapes on quadrants. In rotation questions they will have to rotate a shape by 90°, 180° or 270° around a certain coordinate (not necessarily (1, 1)), and then be able to identify the new coordinates. Translation in this context means moving a shape, for example moving a triangle 2 squares up and 4 squares to the right on a quadrant. Reflecting shapes would involve mirroring them across a certain line on the grid.
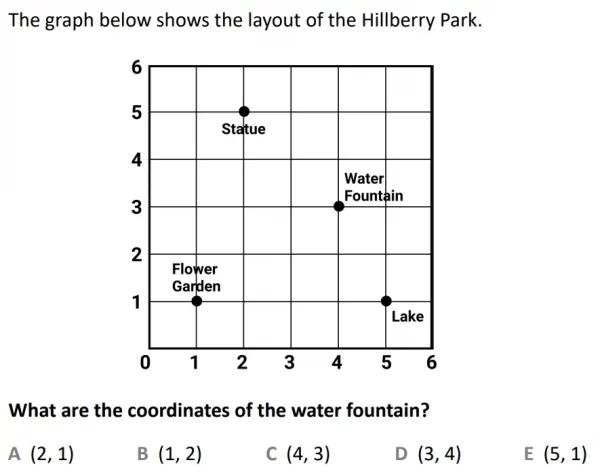
When finding coordinates, we know that the X-axis always comes first. Therefore we know that in the example question, the coordinates of the water fountain must be option C, (4, 3); 4 across on the X-axis and 3 up on the Y-axis.
Type 26 - Mean, mode, median & range
Mean: When we add up all of the numbers in a data set and divide that total by how many numbers there are.
Mode: The number that appears the most in a data set.
Median: The middle number when we order a data set from lowest to highest.
Range: The difference between the biggest and smallest numbers.
In the example question we are told that the mean height, 140cm, is 7 times as large as the range, and we are asked to find the height of the smallest child, with the knowledge that the tallest child is 164cm. Therefore we must divide 140 by 7 to find the range, which is 20. Then we can subtract 20 from the height of the tallest child, 164, to find the height of the smallest child, 144cm (option A).

Type 27 - Probability
Probability can be asked in a number of ways, such as with spinners, playing cards and dice, and it may be presented in different ways, such as as fractions, percentages or numbers (eg a 1 in 6 chance).
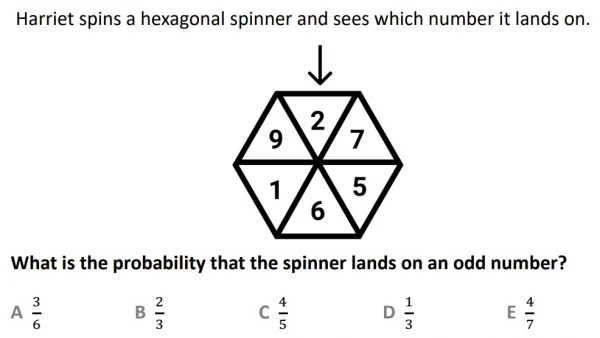
In the example question we are asked to find the probability that a hexagonal spinner lands on an odd number. Since the spinner has six numbers, the possibility that it could fall on any of them is 1/6. Four of the six numbers are odd, meaning that there is a 4/6 chance of it landing on an odd number, and this fraction can be simplified to 2/3, so the answer is option B.
Type 28 - Tables & data handling
Tables and data handling tests your child’s ability to interpret data sets presented in a variety of ways, such as diagrams, bar charts, pie charts, Venn diagrams and Carroll diagrams. This may involve filling in missing sections based on the rest of the data shown, converting data into fractions, percentages, etc, and finding averages based on the data we see.
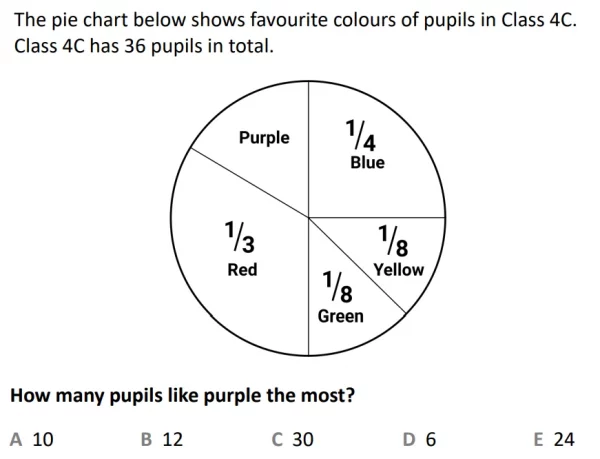
In the example question we’re asked to find how many pupils in a class choose purple as their favourite colour. We’re shown fractions for each of the other colours, and also given the total number of pupils in the class. However some of the fractions we’re given have different denominators, meaning that in order to compare them we must find a lowest common denominator. 8 multiplied by 3 is 24 so we can use that as a denominator. 1/8 becomes 3/24, 1/3 becomes 8/24 and 1/4 becomes 6/24 as we multiply the numerators by the same number that their denominator must be multiplied by to become 24. Then, we can add up all of the numerators to find 20/24. What’s left is 4/24, which can be simplified to 1/6 – the fraction of the 36 pupils whose favourite colour is purple. To find the overall number we can then multiply 1/6 by 36 to get 6 pupils, option D.
Type 29 - Time: durations, 24-hour clock, timetables
Questions to do with time may involve working out what time something ends based upon its start point and duration, converting times from 12 hour to 24 hour clocks, as well as between different time zones, and reading and using timetables.
The key to getting this example question right is understanding how time zones work, and also remembering that there are 60 minutes in an hour, not 100. We’re asked to find what time Abby calls Karl according to Karl’s time zone in New York, which is 5 hours behind Abby’s in London. Abby’ meeting starts at 2:30pm (London time) and lasts 75 minutes, meaning it finishes at 3:45pm – so this is the time that she calls Karl. Then we have to go back 5 hours to get the New York time. When we do this we get to 10:45am, so option E.

And there we have it, all of the 30 possible types of question that could come up in a GL Maths paper. Remember to check out all of the question types and topics from the other 11 plus sections here.
As well as that, our brand new Maths Pack, which features 4 expert-made full-length Maths practice papers, is now available to order! Check it out here.
